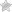Их задача – определить диапазон вероятностей, в котором произойдут те или иные события. Чисто технически, размах прошлых колебаний доходности позволяет вычислить диапазон ее будущей неопределенности. Размах колебаний и неопределенность результатов измеряются стандартным отклонением или дисперсией. В основе этих моделей лежит допущение, что распределение риска описывается кривой Гаусса, названной так в честь открывшего ее математика Карла Фридриха Гаусса.

Другое ее название – «кривая нормального распределения вероятностей» – отражает общепринятый взгляд на это явление. Другое ее название – «кривая нормального распределения вероятностей» – отражает общепринятый взгляд на это явление. Имеется в виду такое распределение, где средняя величина является и самой часто встречающейся величиной.

Точечные скопления данных образуют кластеры в средней части графика. «Нормальное распределение» графически представляет собой кривую в виде колокола с расплющенными краями.

В таких моделях принимается на веру, что диверсификация снижает уровень риска; если у нас много активов, то риски, уникальные для каждого из них, имеют тенденцию к взаимной нейтрализации, так как они в основном не связаны друг с другом. Модели управления рисками игнорируют возможность почти полной корреляции или общих толчков в движении рисков, свойственных периодам бума или краха.